K4Maths

📚 Introduction

Series are a very important topic in further maths, and they are very interesting. I'll be covering the basics of series in this lesson. This includes the notations, and how to read them. We'll also cover some basic types of series, and how to find the sum of a series.

🎯 Learning Objectives

By the end of this lesson, you will be able to:

Understand the basic notation used in series
Identify different types of series
Calculate the sum of a simple series

🔑 Key Concepts

What is a series?

A series (or summation) is just the sum of a sequence of numbers. For example, the series 1 + 2 + 3 + 4 + 5 is the sum of the first five natural numbers.
The way we would write this series is like this: $$\sum_{k=1}^{5} k = 1 + 2 + 3 + 4 + 5$$ This just means: "Add all numbers from $k$, the bottom number (1) to the top number (5)".

📖 Definition

Sigma: The symbol $\sum$ is used to represent the sum of a series. It is followed by an expression that defines the terms to be added.
Like the integral symbol $\int$, the sigma symbol $\sum$ accumulates values, but instead of areas under curves, it adds up discrete terms of a sequence. Similarly, it has two limits, one limit at the top "$n$" and one limit at the bottom "$k=1$".
This is the notation for a series:

\sum_{k=1}^{n} \text{(term that follows)}

Sums of constant terms:

The sum of a constant term (in the below instance is five) is just the constant $\times$ the number of terms.
For example, the sum of: $$\sum^{10}_{k=1} 5$$ is simply $$5 + 5 + 5 + 5 + 5 + 5 ... \text{ten times} = 50.$$
The formula for this is: $$\sum^{n}_{k=1} \gamma = \gamma \times n$$ where $\gamma$ (gamma) is the constant, and $n$ is the number of terms.
Note: $\sum_{k=1}^{n} 1 = n$ because we're adding 1 repeated $n$ times.

💡 Flash question

Solve for the following summations $$\sum_{k=1}^{100} 15 \quad + \quad \sum^{50}_{k=1} 2$$

🔍 Show Solution

Then first summation: $$\sum_{k=1}^{100} 15 = 15 \times 100 = 1500$$
The second summation: $$\sum^{50}_{k=1} 2 = 2 \times 50 = 100$$
So: $$1500 + 100 = 1600$$

The sum of the first $n$ natural numbers

The sum of the first $n$ natural numbers is written as: $$\sum^{n}_{k=1} k = 1 + 2 + 3 + ... + n$$
Looks familiar? Let me explain it clearly. We start at $k=1$ (the bottom number) and we add every natural number from $k$ to $n$ (the top number).
So, for example, if we had: $$\sum^{5}_{k=1} k = 1 + 2 + 3 + 4 + 5 = 15$$
The formula for this is: $$\sum^{n}_{k=1} k = \frac{n(n+1)}{2}$$ Remember, natural numbers are just positive integers ($1, 2, 3, 4, 5 ...$ etc), and denoted as $\mathbb{N}$.

📖 Adding and Subtracting when k doesnt start at 1

Example. Solve: $\sum^{50}_{k=15} k$

\text{Notice } k = 15 \text{ instead of 1}$$ $$\text{So lets split it into two and subtract one from the other}$$ $$\text{lets find from } 1 \rightarrow 50$$ $$\sum^{50}_{k=1} k= \frac{50(50+1)}{2} = 1275$$ $$\text{Now, since we were supposed to start at }15,$$ $$\text{ we can subtract the sum from } 1 \rightarrow 14$$ $$\sum^{14}_{k=1} k= \frac{14(14+1)}{2} = 105$$ $$\text{So, we can do } 1275 - 105 = 1170$$ $$\therefore \sum^{50}_{k=15} k = \boxed{1170}

Let me help you understand this better:

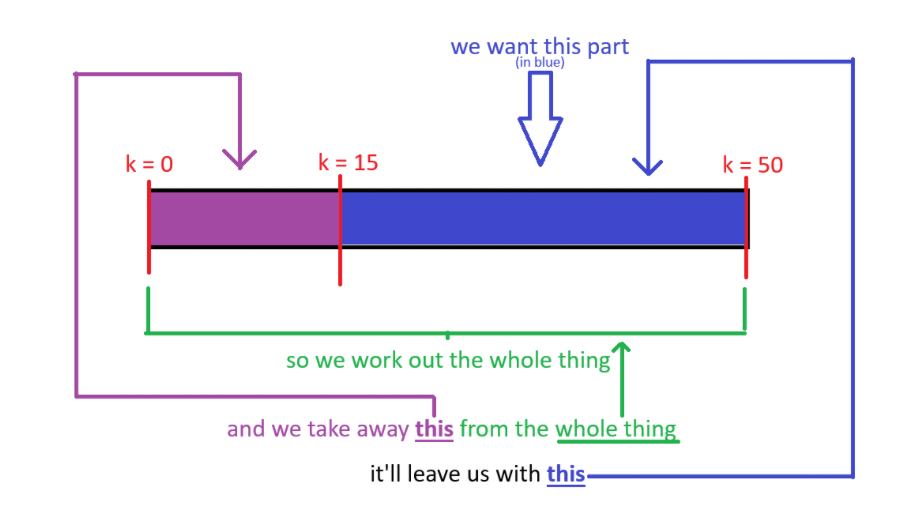
So we found from $\quad 1 \rightarrow 50\quad $ and subtracted $\quad 1 \rightarrow 14\quad $ to get $\quad 15 \rightarrow 50\quad $

We can also have an algebraic series.

For example, $\sum^{4}_{k=1} (2k - 1)$ is an algebraic series.
This means we substitute $k$ with the values from $1$ to $4$ and then add them up.
So, we have: $$\sum^{4}_{k=1} (2k - 1) = (2 \times 1 - 1) + (2 \times 2 - 1) + (2 \times 3 - 1) + (2 \times 4 - 1)$$ $$= 1 + 3 + 5 + 7 = \boxed{16}. \text{ This is the sum of the first 4 odd numbers}$$
Since this series is small, (limit is 4) we can just write it out fully. for longer series, theres a better method:
We can split the summation into two separate summations, similarly to the previous example: $$\sum^{4}_{k=1} (2k - 1) = \sum^{4}_{k=1} 2k - \sum^{4}_{k=1} 1$$
To take it further, since 2 is a constant, we can pull it outside the summation using linearity: $$\sum^{4}_{k=1} (2k - 1) = 2\sum^{4}_{k=1} k - \sum^{4}_{k=1} 1$$
Now, we can substitute the formulas we know: $$2\sum^{4}_{k=1} k - \sum^{4}_{k=1} 1 \quad = \quad 2\left(\frac{4(4+1)}{2}\right) - (1 \times 4)$$ $$ 2\left(\frac{4(4+1)}{2}\right) - (1 \times 4) \quad =\quad 2(10) - 4 = 20 - 4 = \boxed{16}$$
And we get the same answer, as anticipated.

📝 More Worked Examples:

📋 Example 1: Sum of a constant

Question: Show: $$\sum^{2N -1}_{r = 5} r = 2N^2 - N - 10, \quad N \geq 3$$

Solution:

Step 1:

Notice it doesn't start at 1? Let's first split it into two and subtract the part we don't want.

Since we want $r = 5$ to $r = 2N-1$, we can find $r = 1$ to $r = 2N-1$ and subtract $r = 1$ to $r = 4$ (which gives us $r = 5$ onwards).

\sum^{2N -1}_{r = 5} r \quad \text{ Can be written as} \rightarrow \quad \sum^{2N -1}_{r = 1} r - \sum^{4}_{r = 1} r

Step 2:

Now, lets use our formulas we know.

\frac{n(n+1)}{2}\quad \text{ Can be written as} \rightarrow \quad \frac{1}{2}n(n+1)$$ $$\text{So} \rightarrow \sum^{2N -1}_{r = 1} r - \sum^{4}_{r = 1} r= \frac{1}{2}(2N - 1)(2N) - \frac{1}{2} \times4\times(4+1)$$ $$\text{Now, lets simplify the first part and expand brackets:} $$ $$ \frac{1}{2}(2N - 1)(2N) = \frac{1}{2}(4N^2 - 2N) = \boxed{2N^2 - N} $$ $$\text{Now, the second part:}$$ $$\frac{1}{2} \times4\times(4+1) = \frac{1}{2} \times4\times5 = \boxed{10}

Final Answer:

Combine first and second parts:

\text{So, we have:}$$ $$\text{First part - Second part} = \boxed{(2N^2 - N) - 10} \rightarrow \text{proved.}

⚠️ Common Mistakes

🚫 Mistake 1: Forgetting to split Summations into two or more

Splitting the summation is really handy and makes it much easier. If you have a complex summation, try breaking it down into smaller parts.

Why it's wrong: Not splitting the summation can lead to mistakes in calculation and understanding. It’s important to simplify complex problems. Even the best do it.

How to avoid it: Always look for ways to break down summations into simpler parts. Practice this technique with various problems to become more comfortable with it. And ensure you're algebraically correct.

💪 Practice Problems

Try these problems to test your understanding:

🎯 Practice Questions

(A) Evaluate: $$\sum^{4}_{k = 1} (3k + 2)$$
(B) Evaluate $$\sum_{r=21}^{40} r$$
(C) Find n given that $$\sum^{n}_{k=1} k = 528$$
(D) Show that $$\sum^{n}_{r=1} (7r - 4) = \frac{1}{2}n(7n-1)$$

🔍 Show Solution

(A) $$\sum^{4}_{k = 1} (3k + 2) = \sum^{4}_{k = 1} 3k + \sum^{4}_{k = 1} 2 = 3\sum^{4}_{k = 1} k + 2 \times 4 = 3(10) + 8 = \boxed{38}$$
(B) $$\sum_{r=21}^{40} r = \sum_{r=1}^{40} r - \sum_{r=1}^{20} r = \frac{40(40+1)}{2} - \frac{20(20+1)}{2} = 820 - 210 = \boxed{610}$$
(C) $$\sum^{n}_{k=1} k = \frac{n(n+1)}{2} = 528 \Rightarrow n(n+1) = 1056 \Rightarrow n^2 + n - 1056 = 0$$ $$\text{Using the quadratic formula: } n = \frac{-1 \pm \sqrt{1 + 4 \times 1056}}{2} = \frac{-1 \pm \sqrt{4225}}{2} = \frac{-1 \pm 65}{2}$$ $$\text{So, } n = \frac{64}{2} = \boxed{32} \text{ (since n must be positive)}$$
(D) $$\sum^{n}_{r=1} (7r - 4) = 7\sum^{n}_{r=1} r - 4\sum^{n}_{r=1} 1 = 7\left(\frac{n(n+1)}{2}\right) - 4n$$ $$= \frac{7n(n+1)}{2} - \frac{8n}{2} = \frac{7n^2 + 7n - 8n}{2} = \frac{7n^2 - n}{2} = \boxed{\frac{1}{2}n(7n-1)}$$ $$\text{Thus, proved.}$$

🎯 Practice Questions (harder)

(1) (A) Find an expression for $$\sum_{r=1}^{2n-1}r.$$ (B) Hence show that $$\sum_{r=1}^{n}\bigl(2r-1\bigr)=n^{2},\quad n\ge2.$$
Hint: For part (b), split the sum $\sum_{r=1}^{2n-1}r$ into the sum of the even terms plus the sum of the odd terms.

(2) Calculate the sum: $$\sum_{r=1}^{55} (3r - 1)$$

(3) Calculate the sum: $$\sum_{r=1}^{90} (2 - 7r)$$

(4) Calculate the sum: $$\sum_{r=1}^{46} (9 + 2r)$$

🔍 Show Solution

(1)(a) We know the formula for the sum of the first $m$ positive integers: $$\sum_{r=1}^{m}r = \frac{m(m+1)}{2}$$ Here $m=2n-1$. Therefore: $$\sum_{r=1}^{2n-1}r = \frac{(2n-1)((2n-1)+1)}{2} = \frac{(2n-1) \times 2n}{2} = \boxed{n(2n-1)}$$ (1)(b) Split the sum $\sum_{r=1}^{2n-1}r$ into the sum of the even terms plus the sum of the odd terms: $$\sum_{r=1}^{2n-1}r = \underbrace{\sum_{r=1}^{n-1}2r}_{\text{even terms}} + \underbrace{\sum_{r=1}^{n}(2r-1)}_{\text{odd terms}}$$ We have already $\sum_{r=1}^{2n-1}r=n(2n-1)$. Also: $$\sum_{r=1}^{n-1}2r = 2\sum_{r=1}^{n-1}r = 2 \times \frac{(n-1)n}{2} = n(n-1)$$ Hence: $$n(2n-1) = \sum_{r=1}^{n-1}2r + \sum_{r=1}^{n}(2r-1) = n(n-1) + \sum_{r=1}^{n}(2r-1)$$ Rearranging to isolate the odd-number sum: $$\sum_{r=1}^{n}(2r-1) = n(2n-1) - n(n-1) = 2n^{2} - n - n^{2} + n = \boxed{n^{2}}$$ This completes the proof that $\sum_{r=1}^{n}(2r-1) = n^{2}$.

Question (2): Calculate $\sum_{r=1}^{55} (3r - 1)$

Step 1: Split the sum into two separate sums: $$\sum_{r=1}^{55} (3r - 1) = 3 \sum_{r=1}^{55} r - \sum_{r=1}^{55} 1$$ Step 2: Apply the formulas: $$3 \sum_{r=1}^{55} r = 3 \times \frac{55 \times 56}{2} = 3 \times 1540 = 4620$$ $$\sum_{r=1}^{55} 1 = 55$$ Step 3: Calculate the final answer: $$4620 - 55 = \boxed{4565}$$

Question (3): Calculate $\sum_{r=1}^{90} (2 - 7r)$

Step 1: Split the sum: $$\sum_{r=1}^{90} (2 - 7r) = \sum_{r=1}^{90} 2 - 7 \sum_{r=1}^{90} r$$ Step 2: Calculate each part: $$\sum_{r=1}^{90} 2 = 2 \times 90 = 180$$ $$\sum_{r=1}^{90} r = \frac{90 \times 91}{2} = 4095$$ Step 3: Combine: $$180 - 7 \times 4095 = 180 - 28665 = \boxed{-28485}$$

Question (4): Calculate $\sum_{r=1}^{46} (9 + 2r)$

Step 1: Split the sum: $$\sum_{r=1}^{46} (9 + 2r) = \sum_{r=1}^{46} 9 + 2 \sum_{r=1}^{46} r$$ Step 2: Calculate each part: $$\sum_{r=1}^{46} 9 = 9 \times 46 = 414$$ $$\sum_{r=1}^{46} r = \frac{46 \times 47}{2} = 1081$$ Step 3: Combine: $$414 + 2 \times 1081 = 414 + 2162 = \boxed{2576}$$

💡 Problem-Solving Strategy

General approach for algebraic series:

Split complex expressions into simpler summations
Factor out constants from the summation
Apply the standard formulas (sum of constants, sum of natural numbers)
Calculate step by step and combine results

📋 Summary

🎯 Key Takeaways

Summations are written with sigma: $\sum$
We can break them down simpler
We can factor out constants from the summation and find special terms.

📚 What's Next?

I suggest now learning square series - where we have $\sum^{n}_{k=1} k^2$. This is a very useful series to know, and it will come in exams.

⬆️ Back to Top